La Fase: ¿Cómo interpretarla?
La gráfica de fase posiblemente sea la más importante para nosotros a la hora de hacer un ajuste de sistemas de sonido, ya que será la que nos permita encontrar problemas como también será la que nos ayude a poner en tiempo cada uno de los sistemas, porque precisamente en eso se basa: en TIEMPO.
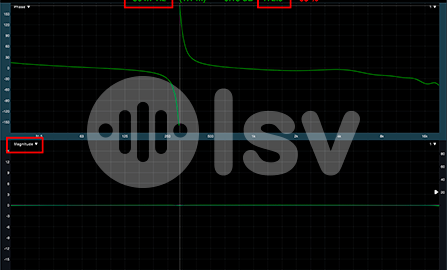
Primero y principal debemos saber que cuando la gráfica es decreciente, indica un retraso y cuando es creciente indica un adelanto.
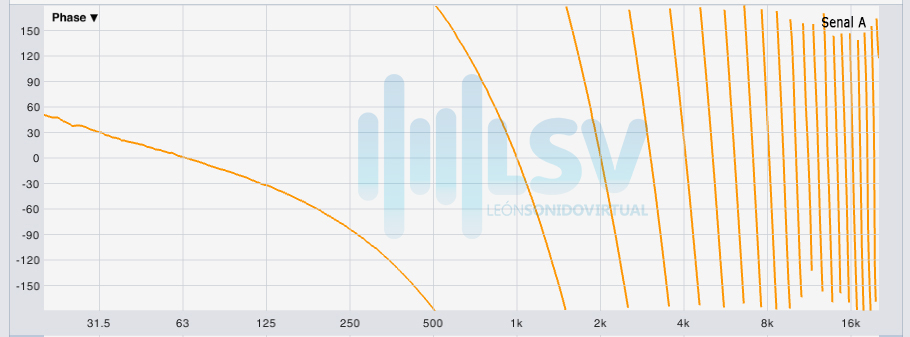
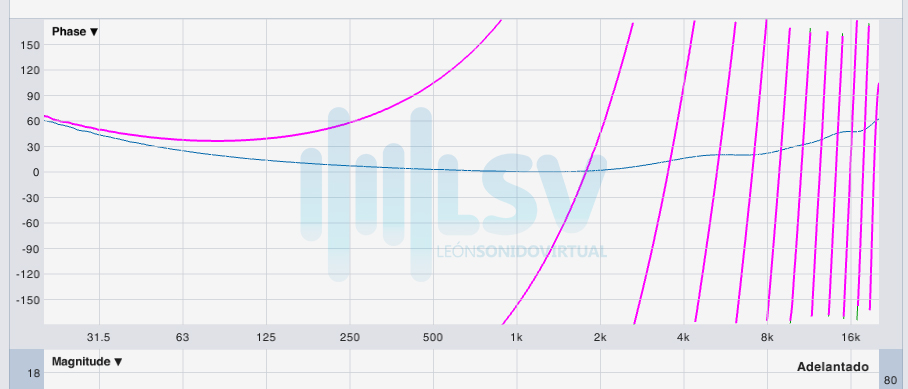
En el post de Comb Filter vimos como calcular el retraso de una señal. En el de hoy, mencionaremos un poco eso.
Para entender de otra manera la información que nos dan estas gráficas de fase veamos dos imágenes.
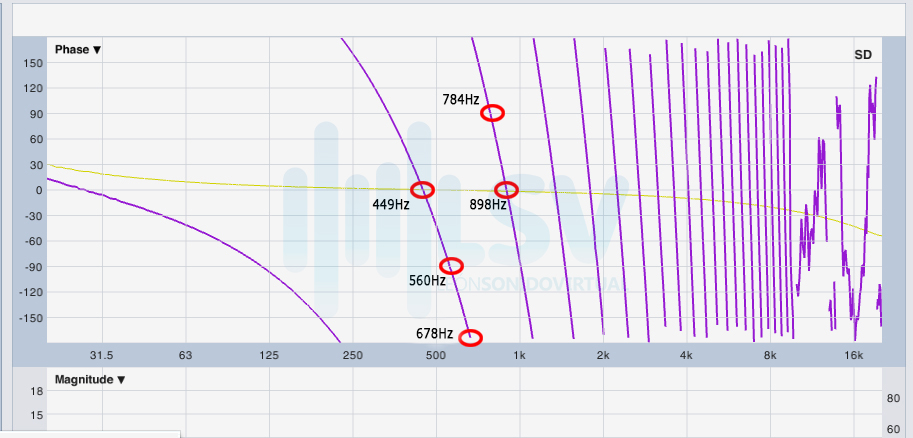
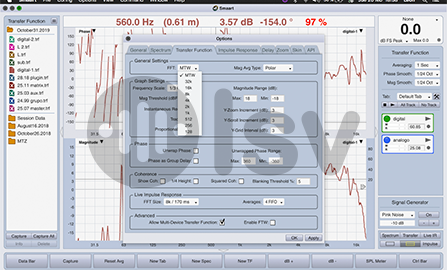
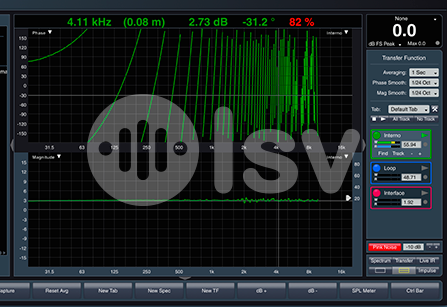
En la figura 3 seleccione 5 puntos equivalentes a 5 frecuencias. Si vemos en el eje vertical de la izquierda encontraremos una escala en grados que va desde -180 a 180.
Entonces acá ya encontramos dos datos importantes: La frecuencia y su desplazamiento en grados. En este ejemplo tome el primer giro completo que equivale a 449Hz y 360 grados. La siguiente frecuencia marcada es 560Hz y si vemos a la izquierda vemos que marca -90 grados. Pero esa frecuencia se encuentra en realidad a 450 grados (360+90) de la referencia. Es decir un ciclo y un cuarto. 678 Hz se encontrara a 540 grados, 784Hz a 630 grados y por ultimo 898Hz a 720 grados (dos giros completos de la referencia).
Como vimos en el post de Comb Filter, podríamos calcular el tiempo de retraso de la señal usando el primer giro completo que equivale a 449Hz.
1/449 = 0,00222 seg ó 2,22ms
Esa es la forma fácil. Si quisiéramos complicarla deberíamos entender lo siguiente:
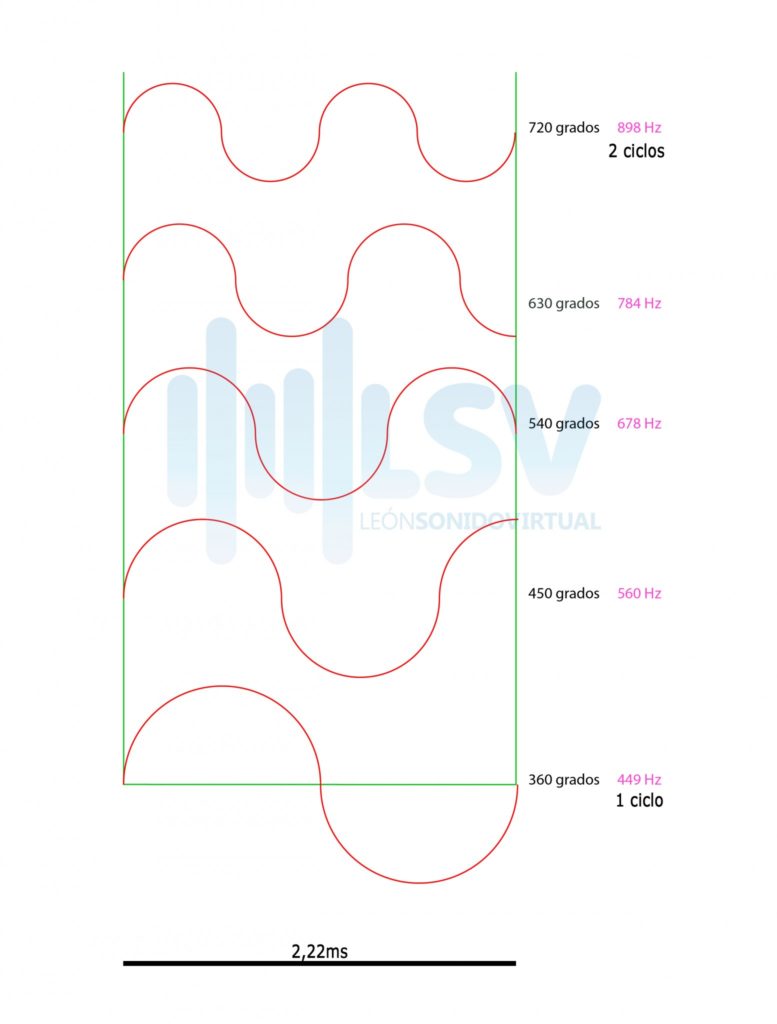
Nuestra señal se ha retrasado una longitud de onda de 449Hz. Por eso simplemente calculando el tiempo equivalente a 449Hz sabremos de cuanto es este retraso.
También podríamos pensar que la señal esta retrasada una longitud de onda y media de 678Hz (540 grados)
1/678 = 0,00147 seg
sumado a la media longitud de onda:
0,00147/2 = 0,00073
Entonces:
0,00147 + 0,00073 = 0,0022 ó 2,2ms
Obtendríamos el mismo resultado usando el criterio explicado.
Si queres saber como aplicar esto en situación acústica de sistemas de sonido mira esta info (Clic Acá)